Why the uncertainty principal does not influence the results of scientific experiments.

When researching a topic as technical and in-depth as the uncertainty principal, one can draw distorted, or even erroneous conclusions about its implications if they haven’t first gained the crucial, but perhaps boring, background knowledge that would help them to better visualize these counter-intuitive ideas in a way truly representative of what has actually been discovered. If I were to look at the wikipedia page on the uncertainty principal, I would find this:

“In quantum mechanics, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle known as complementary variables*, such as position x and momentum p, can be known simultaneously. For instance, in 1927, Werner Heisenberg stated that the more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa.”

(*the actual term is ‘conjugate variables’ but whatever same thing)

And then they would see this equation, where ħ is the reduced Planck constant.

…ok dafuq does all that mean?

It’s unfortunate that so many fascinating subjects in science often require years of prior learning in less fascinating, more trivial areas in order to be able gain a reasonably firm understanding of those discoveries which are mind-bending, and rife with profound philosophical and/or spiritual implications. It turns people off to the notion of getting involved with science if they feel apprehensive about having to sift through all the boring prerequisites before they get to anything interesting. Math is definitely a turn off for most people, but not to worry. I never really stood out in math class; typically my best grades were in the B range, with the majority of them reflecting just the bare minimum to get by… Fortunately, one does not need to be a mathematician in order to understand the essence of the uncertainty principal.

That being said, there is one small caveat: that is, quantum physics as a whole is entirely counter-intuitive. Despite not needing to be a mathematician to understand the essence of many of the phenomena, it does require a certain degree of cleverness/out-of-the-box type thinking.

WHY SO…. uncertain?

If you haven’t heard of the uncertainty principal, it’s often stated in simple terms as something like, “The act of observation affects the outcome of the experiment.” Thus we cannot be certain that our result is truly representative of reality. But this is a very, very simplified explanation that inevitably leads to some critical misconceptions. The uncertainty principal is an inherent property to all waves, as explained in this short video:

http://www.youtube.com/watch?v=7vc-Uvp3vwg

The notion that the outcomes of experiments are influenced by the act of observation is likely a result of misinterpreting what’s going on at the subatomic level.

It is necessary to describe what happens during an observation at the quantum level and what happens during an observation at our human level. When someone observes something in our familiar macroscopic world, the effect they have on the object of observation is so infinitesimally small that it’s completely negligible and immeasurable. For example, if I wanted to check the air pressure in my tire, I would need to release a tiny amount of air into my pressure gauge to see exactly what PSI they’re at. But in so doing I decrease the pressure in my tire by a tiny bit—a fraction of a fraction of a single PSI—but nonetheless affecting the result of my ‘experiment’.

Another way to observe something is to simply look at it. Lets say I wanted to do a study in early child development (as used in an example for a question a friend asked me regarding this whole topic), I’d observe the infant by collecting the photons that bounced off his/her body in my retinae, and then recording what it was that i saw (behavior, temperament, play habits, level of social skills, etc). For my observation to affect the outcome in this experiment, as a result of the uncertainty principal and not shortcomings in the design of the experiment, the infant’s ability to engage in those activities would be acted upon in a physical way—as if being unable to play because of a powerful stream of air, like a jet engine blowing in its face, restricting proper use of motor skills, affecting mood, behavior, temperament, etc.

But we can all see that, unlike high-speed oxygen molecules, the photons bouncing around our atmosphere do not have this effect on anyone, despite hurtling at our faces at the speed of light 24/7. Bouncing photons off an infant does nothing to affect what it is the experimenter may be testing for, and that is an important distinction to make.

Outcomes changed/influenced by observation?

If a physicist wanted to observe the position and momentum of an election, the normal way of observation—to simply look at it—does not work. At the quantum level “looking” means to bounce photons off of something and collect them in your retinae (or whatever finely tuned optical instrument you may be using), but after a certain point, things just get too small to see. The tiny object does not have enough surface area to reflect the minimum number of photons necessary to be detected by your naked eye. With help from a microscope we can see these things, but what happens when the object is too small for the microscope?

An electron and a photon are roughly the same size; both are considered “point particles”, thus to bounce a photon off an electron is very similar to hitting the 8-ball with the cue ball. In order to measure the momentum, you inevitably must affect its position; in order to measure its position, you inevitably must affect its momentum. Such pairs of properties that behave in this way are known as “conjugate variables” (as noted in the beginning) and are of course not limited to just position and momentum.

This is not the result of shortcomings with observational technology. This is a universal, fundamental property in all wave-like systems, and it arises in particle physics because of the matter-wave nature of all quantum objects. It’s important to note that the uncertainty principal really doesn’t play a role in affecting outcomes/results outside of the quantum realm. Even on microscopic scales such as in cell biology and computer chip manufacture, the uncertainty principal does not influence results of those experiments. The fundamental particle level is yet many millions of times smaller than that. But to really understand why the uncertainty principal only works at the quantum level, requires an understanding of the role of the observer.

And understanding the role of the observer first requires an explanation of what superposition is, and to understand superposition requires an explanation of the double slit experiment.

Double-slit experiment and interference patterns

Thomas Young’s double-slit experiment actually belongs to a wider group of “double path” experiments that involve splitting a wave into two separate waves that later rejoin to become a single wave. First, lets examine the single-slit experiment.

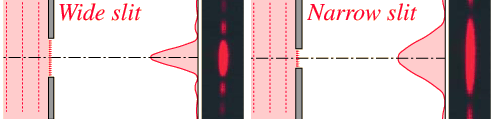
An apparatus is constructed that fires a laser beam through a narrow slit onto a white screen. The original hypothesis was that, as the slit narrowed, so would the width of the laser beam. But instead, to the confusion of the experimenters, the beam grew wider, like this:

http://www.youtube.com/watch?v=a8FTr2qMutA

If you feel the title of that video didn’t live up to expectations, then I agree. But it’s a simple, clear example of how these slit experiments are set up.

The beam doesn’t get narrower because the photons are essentially behaving like waves; consider a wave in the ocean as it hits a barrier with a single opening. From a top-down view you would see the wave radiating out from the opening in a semi-circle shape:

This is known as “single slit diffraction”. When the peaks and troughs of the wavelengths of light hit the screen at the same time, it is known as “arriving in phase”. This produces what’s called “constructive interference”, which we are able to see as the widening of the laser beam. However, when the peaks arrive simultaneously with the troughs, the wavelengths then cancel each other out, leaving us with a dark spot, called “destructive interference”:

 

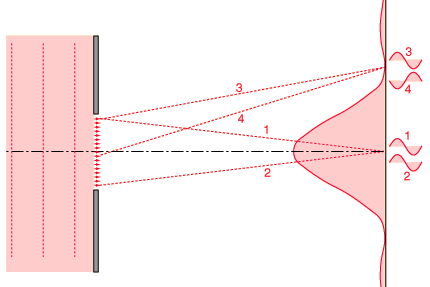
It was early in the 19th century, and at the time this observed phenomenon was quite a mystery to physicists—many of whom supported the particle theory of light, published by Sir Isaac Newton in 1704. Although Christiaan Huygens proposed a wave theory of light in 1678, some did not accept it due to reasons which require a confusing, technical explanation…

(In short: longitudinal waves cannot show birefringence, which is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light. These optically anisotropic materials are thus said to be birefringent.) wut o_O

So what would happen if we added a second slit? Back in the 1800’s everyone predicted there would be two separate lines of light; an entirely logical hypothesis considering people generally thought of light as a stream of particles, and seeing two separate lines would’ve confirmed their hypothesis. But instead of seeing that, an interference pattern was observed:

What was causing all that extra destructive interference? The answer to this question effectively takes us to…

SUPERPOSITION DOOD

Christiaan Huygens turned out to be right. There was no way around it; the only way results like these could be possible was if light behaved like a wave. Though he did not live to see it, Huygens managed to get the last laugh against Sir Isaac Newton.

…Or did he?

The screen detected points of interference, the likes of which are characteristic of particles. Yet, they aggregated in such a way that produced the interference pattern expected of a wave. Both men turned out to be right, which is precisely the reason why this shit is so fucking goddamn batshit crazy.

 

So the experimenters have results indicating particles behaving like waves; why is that so batshit crazy? Because in order to produce the interference pattern, the wave must pass through both slits simultaneously. If we go back to our beach wave analogy it’s easy to visualize how a wave passes through two openings at once. But the detector clearly picked up particles, and how could a particle pass through two separate openings at the same time?

Even when the rate of fire was decreased to a single photon at a time, the same interference pattern showed up on the detector. Therefore, the particle must fire from the laser, pass through both slits at once, interfere with itself, and then get picked up by the detector at a single point.

What in the world can account for this seemingly impossible behavior? Well, the photon is something unlike human beings have ever encountered before, and it’s important to gain an appreciation of that. Our minds simply did not evolve to understand this type of thing.

Once the photon leaves the light source, it behaves as though it has all possible values for a given property. It would be as if a pitcher threw a baseball, and as soon as it left his hand, instead of one baseball zooming straight into the catcher’s mitt, a wave of baseballs occupying that entire region of values would zoom into the catcher’s mitt. But as soon as it interacted with either the bat or the glove, it would be reduced back to a single value.

This wave of baseballs—our stand-in photons—is not the same as a familiar beach wave. Instead of a wave of water molecules, it is a wave of probability. The greater the amplitude of the wave, the greater the probability of finding a baseball at that position. You can imagine I’d be wasting my time trying to perform a measurement behind the pitcher, since the amplitude of the wave would be so tiny that the chances of me finding a baseball there would be virtually zero. In other words, the size of the wave at any given point predicts the likelihood of finding a photon at that location.

This is the essence of superposition. It cannot be said that the particle exists at this location or that location; the particle occupies all possible positions (thus referred to as being in a state of superposition) with increased likelihood of being found where the amplitude of the wave is highest.

This is how the photon passes through both slits at the same time. Once it leaves the light source (and before we can measure it), it exists in this weird state of superposition, with the size of the probability wave at the narrow slit openings being equal. The probability wave then radiates out from the two openings in the aforementioned semi-circular shape, interferes with itself—producing the interference pattern—and finally hits the collection screen.

If you recall, once the measurement has been performed, the multi-valued state of superposition disappears and is reduced to a single value; the photon has what’s called a collapsed wave function. Which finally brings us back to…

The Role of the Observer

In basic terms, the role of the observer collapses the wave function of the photon. Knowing the Heisenberg uncertainty principal is a fundamental property in all wave-like systems, and knowing the role of the observer collapses the photon’s wave function, we can now put two and two together and come to the obvious conclusion: particles that are “observed” are no longer affected by the uncertainty principal. But what exactly makes an observation? And how can the act of observing collapse a particle’s wave function?

In the documentary, “What the Bleep do We Know?” (spelled out with clever symbols and what not) there was a 5-min portion of the film explaining the double-slit experiment, but it put a slight spin on the results with spiritual—or perhaps more erroneously—mystical undertones. But there is nothing mystical about quantum physics; it is certainly bizarre and counter-intuitive, but these phenomena are pretty well understood and accurately modeled by equations developed by Shrodinger, Heisenberg, Planck, etc.

The spiritual/mystical element comes in when the experimenters move the detector to the site of the two slits. Before, the screen was effectively making the observation, but now the observation occurs at the two openings, thus the wave function of the photon (or electron or whatever particle) gets collapsed sooner, at which point the particle behaves just like a particle. The visible effect is that the interference pattern disappears and we are left with two separate, clearly defined lines. This was quite a conundrum for the physicists at the time for sure, but notice the way it’s portrayed in the movie:

http://youtu.be/fwXQjRBLwsQ?t=3m53s

“The electron decided to act differently as though it were aware it was being watched…”
Now, I’m all for the use of metaphors to convey a complex idea in simple terms, but that statement can be very misleading.

“What does an observer have to do with any of this?”
This is actually not a mystery and is in fact extensively researched. An “observer” does not need to be a conscious human being, nor does it need to be an instrument constructed for observation by a human being. The implication in the “What the Bleep” video that “it was aware it was being watched” because of the mere act of observing, is probably the result of doing just enough research into the topic to sound like an expert to all the non-experts (and people who don’t bother to dig deep).

There is a natural assumption we humans make (as a result of being at the mercy of our evolutionary biology) that there is a distinction between “observing” and “being observed”. Nature does not make such a distinction. As far as nature is concerned, “observing” and “being observed” is just an interaction between two bodies. Therefore, an observer can be an inanimate object. From nature’s perspective, it is just as valid for an inanimate object to observe a conscious being as it is for a conscious being to observe an inanimate object.

Once the particles involved in this interaction we humans have labeled “observation” interact, the wave function collapses. On the microscopic scale this means any molecule existing on its own is technically “observed”, since the interaction of its electromagnetic bonds collapses the wave function of the subatomic particles. On the macroscopic scale, everything we can perceive is comprised of molecules and compounds, and are technically “observed” even before we interact with them via our senses.

What does this mean for the rest of science???

This means the Heisenberg Uncertainty Principal does not influence the results of scientific experiments :D!!!!! Unless, of course, that scientific experiment happens to be a double-path experiment, or some such other quantum physical experiment that involves particles being in a state of superposition. But in our everyday macroscopic world of scientific experimentation, you can rest assured that those results are in fact reliable and are not subject to the uncertainties of the uncertainty principal.

To review:

• The Heisenberg uncertainty principal is an inherent property to all wave-like systems (see first video). There is a limit to how much we can know about a wave’s properties.
• The bizarre things we detect at the quantum level are a result of particle-wave duality, which does not occur at the macroscopic level.
• These waves are probability waves, not the wavelength of light determining the energy of the photon (visible light, ultraviolet, x-ray, etc).
• Before we make a measurement, the particle exists in a state of superposition, occupying all values for a property, the highest likelihood of which exist where the amplitude of the probability wave is highest.
• Once the measurement is performed, the wave function collapses and the particle takes a single value. (Role of the observer.)
• Now that the particle has been observed and its wave function collapsed, the uncertainty principal is no longer a factor.
• An observer does not need to be a conscious human, nor does it have to be an instrument constructed for observation by a conscious human. An observation from nature’s point of view, and in the technical sense, is simply an interaction between two bodies.
• Macroscopic objects in our everyday world are comprised entirely of ongoing quantum interactions that collapse the wave functions of its constituent subatomic particles, which is why we don’t see all the stuff around us as being in a state of superposition.
• Finally, this means the uncertainty principal does not play a role in influencing the results of scientific experiments in our familiar, macroscopic world—and that our science and our data and our results and our equations are, in fact, sound and continue to make accurate predictions about the crazy freakin universe we live in!

SCIENCE FTW!